Impossible 4-D Quadrilateral

Just as the impossible triangle is a two-dimensional drawing of an impossible 3D object, this model is a 3D representation of something that a person living in 4D would consider an impossible quadrilateral. Scott Kim (of "inversions" writing fame) invented this model and explained it brilliantly in a journal article. Kim wrote his article in two parallel sections. In the first section, he explained the properties of the impossible triangle and what gives rise to the illusion. In the next section, he uses the same structure and even many of the same sentences to describe the 4D illusion. Even though we can't visualize 4D, reading Kim's article gives us an appreciation for the 4D illusion.

Steps

1. Cut out the pattern pieces out of paper or card stock.
   
2. Score and fold two pieces with mountain folds and two pieces with valley folds. Glue the pieces to make two "left-hand" pieces and two "right-hand" pieces.
   
3. Nestle the four pieces together to form the 3-D model of the 4-D illusion.
   

Notes

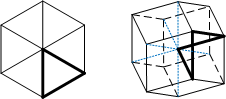• This illusion is related to the impossible triangle. You can understand this model better by seeing how they are analogous. An impossible triangle is based on the isometric projection of the cube. The impossible 4D quadrilateral illusion is based on the isometric projection of the 4D cube (tesseract).
  
• When viewed from a certain angle, each piece of this model resembles the impossible triangle.
  

References

• (Kim 1978)